miércoles, 14 de septiembre de 2011
Temas para repaso en Geometría
Teorema de Tales
Teorema de Tales 1
Ejercicio Teorema de Tales
Semejanza
Semejanza de triángulos 1
Semejanza de triángulos 2 principio práctico
Teorema de Pitágoras
Teorema de Pitágoras 1
Taller tipo ICFES Cuarto Periodo
sábado, 27 de agosto de 2011
PROBABILIDAD
CONCEPTOS BASICOS QUE SE UTILIZAN EN PROBABILIDAD (experimento, espacio muestral, evento )
DIAGRAMA DE ARBOL (Grafico que representa un espacio muestral de una serie de experimentos)
EJEMPLOS1 -PROBABILIDAD DE UN EVENTO SIMPLE
EJEMPLO 2 - PROBABILIDAD
sábado, 16 de julio de 2011
TERCER PERIODO

Proporción : es la igualdad entre dos razones así a/b = c/d donde b y d son diferentes de cero
OBJETIVO
Usar conceptos básicos de probabilidad
Materiales:
 Nota : Lee la siguiente (lectura) información te servirá para responder algunas preguntas de la sesión 2 .
Nota : Lee la siguiente (lectura) información te servirá para responder algunas preguntas de la sesión 2 . ¿Cómo surgió? El Reconocimiento de figuras semejantes ha sido un recurso utilizado desde tiempos inmemorables para la determinación de algunas medidas o para el cálculo de área y de volumen de ciertos cuerpos. En los papiros egipcios y en las tablillas babilónicas que se han hallado, aparecen planteados algunos problemas en los que se evidencia que ya tenían los conocimientos de semejanza.
En que se aplica?

Figuras Congruentes: Tienen la misma forma y la misma área. También se entiende que dos figuras son congruentes si existe una isometría que transforma una figura en la otra. Figuras Equivalentes: Tienen distinta forma pero la misma área.
Figuras Semejantes: Tienen la misma forma pero área diferentes (proporción, tamaño diferente). Los criterios en matemática para que dos o más triángulos sean semejantes son:
Taller 2
Sesión 3: Medición práctica de campo
Sesión 4 : La circunferencia
lunes, 13 de junio de 2011
Estadística proyecto
ENCUESTA ESTADISTICA GRADO NOVENO
Cali, 14 de Junio del 2011
Taller en grupo
0. Para este trabajo se tendrá en cuenta el ser (disciplina, responsabilidad, colaboración, atención), saber- hacer(presentación de trabajo, uso de las tic, el uso de Excel para realizar, procesar , envió información por internet)
Cada grupo conformado deberá:
1. Copiar en el cuaderno el tema que le corresponde elaborar
2. Realizar encuesta para cada uno de los estudiantes de su grado, organizar los datos para posteriormente trabajarlos en Microsoft office Excel. (Tenga presente por cada estudiante debe hacerle dos preguntas y el total de encuestados debe coincidir con el total de estudiantes de su grado al que corresponde
3. Organizar este trabajo en la hoja electrónica Excel teniendo presente la explicación dada por la docente quía
4.Cada estudiante debe copiar en el cuaderno la tabla de FRECUENCIA , histogramas
5. Presentar este trabajo en Excel para ser calificado en estadística
6. Enviarlo por correo karseyer@gmail.com en la fecha establecida escribiendo los nombres y apellidos y grado de los que conforman el grupo de trabajo.
Grupo 1
 Grupo 2
Grupo 2 Grupo 3
Grupo 3 Grupo 4
Grupo 4 Grupo 5
Grupo 5
Tenga en cuenta para el anterior trabajo la siguiente teoría:
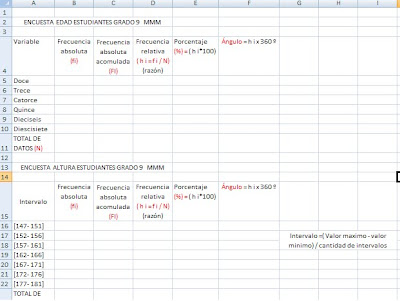
Un histograma es una representación gráfica de una variable en forma de barras(colunnas verticales), para mostrar las frecuencias las cuales no debe haber espacios entre barras. Se utilizan para variables continuas o para variables discretas, con un gran número de datos, y que se han agrupado en clases.
Tablas, frecuencias y gráficos
1. Ejemplo de una variable cuantitativa discreta
En un examen, la calificación máxima es 10 y la mínima es 0.
Las notas de del examen de matemáticas de 30 alumnos de noveno son las siguientes:
5, 3, 4, 1, 2, 8, 9, 8, 7, 6, 6, 7, 9, 8, 7, 7, 1, 0, 1, 5, 9, 9, 8, 0, 8, 8, 8, 9, 5, 7.
a) Ordenar los datos y calcular las frecuencias.
b) Hacer un diagrama de barras de las frecuencias absolutas y dibujar el polígono de frecuencia.
Solución:
a) Cálculo de frecuencias
Ordenamos los datos contando los alumnos que han sacado un 0 han sido 2, un 1 han sido 3 y así sucesivamente. Construimos la tabla correspondiente:
N: número total de datos N = 30.
xi: variable estadística, nota del examen.
fi: frecuencia absoluta, número de veces que se repite una nota. El sumatorio nos da los datos totales N = 30.
FI: frecuencia absoluta acumulada. F 2 = f 1 + f2= 2 + 3 = 5 F 3 = F 2 + f 3 = 5 + 1 = 6
hi: frecuencia relativa. Cociente f i / N
HI = frecuencia relativa acumulada
todos los datos de la columna correspondiente)
2. Ejemplo de un diagrama de sectores
En un hipermercado se han producido las siguientes ventas en euros: juguetes 125, plantas 175, discos 250, alimentación 450.
a) Calcular las frecuencias, porcentajes y ángulo correspondiente.
b) Realizar un diagrama de sectores.
a) Colocamos los datos en una tabla.
Las variable xi son los productos vendidos.
Las frecuencias absolutas f i son las ventas de cada producto.
Las frecuencias relativas h i se obtienen dividiendo las frecuencias absolutas entre el total de 1000
El porcentaje se calcula multiplicando la frecuencia relativa por 100.
Para realizar el diagrama de sectores necesitamos conocer el ángulo. Para hallar el ángulo multiplicamos la frecuencia relativa por 360 º que se corresponden con el total.
* Para hallar el ángulo a partir del porcentaje, dividimos entre 100 y multiplicamos por 360º
Poligono: Es un grafico que se realiza a través de la unión de los puntos mas altos de las columnas de un histograma

3. Intervalo de clase
Construcción de una tabla con Intervalos de clase
3, 15, 24, 28, 33, 35, 38, 42, 43, 38, 36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27, 47, 39, 37, 34, 32, 35, 28, 38, 41, 48, 15, 32, 13.
Los intervalos de clase se emplean si las variables toman un número grande de valores o la variable es continua.
Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente.
Límites de la clase
Cada clase está delimitada por el límite inferior de la clase y el límite superior de la clase.
Amplitud de la clase
La amplitud de la clase es la diferencia entre el límite superior e inferior de la clase.
Pasos para hacer la tabla y los intervalos :
1º se localizan los valores menor y mayor de la distribución. En este caso son 3 y 48.
2º Se restan y se busca un número entero un poco mayor que la diferencia y que sea divisible por el número de intervalos de queramos poner.
Es conveniente que el número de intervalos oscile entre 6 y 15.
En este caso, 48 - 3 = 45, incrementamos el número hasta 50 /5 = 10 intervalos.
Otra manera de formar los intervalos es 50 / 10 intervalos = 5
Se forman los intervalos teniendo presente que el límite inferior de una clase pertenece al intervalo, pero el límite superior no pertenece intervalo, se cuenta en el siguiente intervalo.
 Histograma
Histograma
domingo, 24 de abril de 2011
SEGUNDO PERIODO
Sesión uno: Rectas y Ángulos
Objetivo:
Clasificar ángulos según su medida y posición
Reconocer las propiedades fundamentales de los ángulos especiales y establecer relaciones deductivas entre ellos
Materiales:
Escuadra, transportados, material guía-taller, cuaderno, lápiz, internet, computador, blog geometría grado 9
1. Sacar fotocopias de guía y taller
2. Ver, estudiar, repasar tema visto Rectas y Ángulos
3 estudiar rectas paralelas cortadas por una secante
4. quiz5. Entregar resuelto el taller teórico-práctico propuesto en la fecha indicada por el docente guía

Sesión dos: Razones y proporciones
Objetivo:
Utilizar los criterios de razones y proporciones en ejercicios propuestos
Materiales:
Escuadra, transportados, material guía-taller, cuaderno, lápiz, internet, computador, blog geometría grado 9
1. Sacar fotocopia de guía taller
2. Repasar los temas vistos de razón, razones y proporciones, ejercicios propuestos de razones y proporciones
3. Entregar resulto el taller propuesto
4. Quiz
Sesión tres: Triángulos
Objetivo:
Reconocer las líneas y puntos notables de un triangulo
Materiales:
Escuadra, transportados, material guía-taller, cuaderno, lápiz, internet, computador, blog geometría grado 9
1. Repasar triangulos, tipos de triangulo según sus lados y según sus ángulos
2. Entrega de material fotocopiado
3. Ejercicio teórico practico individual y/o en grupo
Sesión cuatro: Estadística
Objetivo:
Elaborar histogramas de frecuencia proyecto así somos
Población y muestra (Proyecto así somos)
Temas:
Caracterización de la variable cuantitativa, tabla de frecuencias, histograma de frecuencia, ojivas
Materiales:
Escuadra, material guía-taller, cuaderno, lápiz, internet, computador, programa Excel, blog geometría grado 9
1. Sacar fotocopia material guía-taller
2. Ver video, repasar y Tomar apuntes en el cuaderno de conceptos básicos de estadística Nociones preliminares.
3. Elaborar encuesta en el aula Variables (edad ?, altura?, peso?, barrio donde vive?, número de personas con quien vives?, vives en casa propia (si o no), la mayor parte de su tiempo libre en que lo dedicas?, ¿Cual es la persona que esta mas al tanto de su formación?
4. Organizar datos en tabla de frecuencia
5. Representar información en diagramas de barras usando programa en Excel
6. Consultar temas propuesto y entregar resultados de la información sistematizada
Sesión 5: evaluación, autoevaluación, coevaluación
PRIMER PERIODO GEOMETRIA GRADO NOVENO
Sesión uno: Magnitudes e instrumentos de medida
Objetivo:Realizar mediciones con instrumentos para diferentes magnitudes físicas
Usar las tic para la enseñanza interactiva de los temas propuestos en geometría
Materiales: computador, internet, fotocopias, rubrica, cuaderno de apuntes
1.Tablas de conversion : al darle Clic a tabla de conversión podrás realizar conversiones de diferentes magnitudes ingresa a ella y compruébalo
2. Realizar el Experimento interactivo de masa(peso), volumen, densidad debes dibujar, tomar apuntes y anotar la respuesta en el cuaderno y en el aula socializar tu trabajo.
Sesión dos: Ejercicios propuestos
Objetivo:Resolver los siguientes problemas de magnitudes utilizando unidades de medida
Materiales: computador, internet, fotocopias, rubrica, cuaderno de apuntes
1. Resolver los siguientes problemas en el cuaderno
a. Si un paquete de caramelos pesa 125 g. ¿Cuántos paquetes del mismo peso puedo formar con 5 kg de caramelos?
b. Un señor vende 143 litros de vino de un recipiente de madera, que contiene 300 litros. Se le derraman del recipiente de madera 7 litros. ¿Cuántos litros le quedan?
c. Una caja contiene 120 manzanas. Si el peso medio de una manzana es de 75 g. ¿Cuántos kg pesarán todas las manzanas?
d. Un barco transporta 2800 toneladas de mercancía. ¿Cuántos vagones harán falta para transportar esa mercancía si cada vagón carga 1400 kg?
2. Tarea Consultar:
a) ¿Que son rectas paralelas?
b) ¿Que son rectas perpendiculares?
c) ¿Que son polígonos? dar ejemplo
d) ¿Que son poliedros?
e) ¿Que objetos de la vida cotidiana asimila o relaciona usted con las siguientes clase de sólidos (de forma de esfera, de forma de cono, de forma de cilindro, de forma de pirámide, de forma de poliedros), nómbralos (mínimo 3 por cada grupo)y organízalos por grupo.
Sesión tres :Taller práctico de medición
Objetivo:Realizar mediciones con instrumentos para diferentes magnitudes físicas.
Usar las tic para la enseñanza interactiva de los temas propuestos en geometría
Materiales: computador, internet, fotocopias, cuaderno de apuntes, regla, multimetro, pesa, termómetro flexómetro, , rueda, caja rectangular, cilindro, resistores fijos, taller quía
1. Ingresar al área virtual y repasar los temas de perímetro, área, volumen2. Realizar el taller práctico individual
3. Elaborar en grupo taller práctico propuesto en el aula de clase y entregarlo resuelto para ser calificado y posteriormente adicionarlo al block ( mediciones con regla, flexómetro, texter)
Sesión cuatro :evaluación, autoevaluación, coevaluacíon, recuperación
Objetivo:Realizar mediciones con instrumentos para diferentes magnitudes físicas.
Materiales:computador, internet, fotocopias, cuaderno de apuntes, regla, multimetro, pesa, termómetro flexómetro, , rueda, caja rectangular, cilindro, resistores fijos, taller quía
Usar las tic para la enseñanza interactiva de los temas propuestos en geometría
1 Taller teórico - práctico
2. evaluación
Todo sobre Aprende - Repaso de los constructos Matemáticos
viernes, 28 de enero de 2011
GEOMETRIA GRADO NOVENO
Para facilitar el entendimiento de los contenidos en el área geometría grado noveno los temas principales tratados se organiza por periodos.
1 PRIMER PERIODO2 SEGUNDO PERIODO3 TERCER PERIODO
4 CUARTO PERIODO
Atte: Carlos A, Castro R.
domingo, 31 de mayo de 2009
Didáctica aprendiendo Geometría
Una parte importante de la geometría plana son las construcciones con regla y compás.
Unidad Geometria Euclidiana ( Guía virtual)

